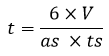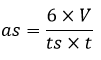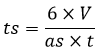Gambar dan Rumus Volume Bangun Ruang

Banyak orang mengetahui macam macam bangun ruang seperti balok, kubus, tabung, bola, dan lain sebagainya. Namun kebanyakan kurang mengetahui Pengertian atau devinisi apa itu Bangun Ruang. Oleh karena itu mereka mencari informasi di internet terkait contoh soal bangun ruang, rumus bangun ruang, gambar bangun ruang dan namanyam, contoh soal luas permukaan bangun ruang, rumus volume bangun ruang, sifat-sifat bangun ruang, jaring-jaring bangun ruang, dan rumus bangun ruang dan bangun datar.

Dikutip dari saintif.com, bangun ruang dapat diartikan sebagai bangunan yang secara matematika mempunyai volume atau isi. Bisa juga diartikan bahwa bangun ruang adalah sebuah bangun tiga dimensi yang mempunyai volume atau isi ruang serta dibatasi oleh sisi-sisi.

Masing-masing bangun ruang tersebut memiliki rumus volume dan luas permukannya masing-masing. Agar siswa dapat mengenal, mengingat dan menyelesaikan berbagai soal yang berhubungan dengan bangun ruang, berikut ini Admin berikan daftar lengkap rumus bangun ruang di bawah ini.

Daftar Bangun Ruang:

1. Kubus

Pengertian / definisi Kubus: Kubus adalah bangun ruang tiga dimensi yang dibatasi oleh enam bidang sisi yang kongruen berbentuk bujur sangkar. Kubus memiliki 6 sisi, 12 rusuk, dan 8 titik sudut. Kubus juga disebut dengan Bidang enam beraturan, selain itu kubus juga merupakan bentuk khusus dalam prisma segi empat, Kubus.

Volume kubus	:  V = s x s x s
Luas permukaan kubus	:  V = s x s x s
Keliling kubus	:  K = 12 x s
Luas salah satu sis	:  L = s x s

Keterangan:

V	: volume
s	: sisi
K	: keliling
L	: luas

2. Balok

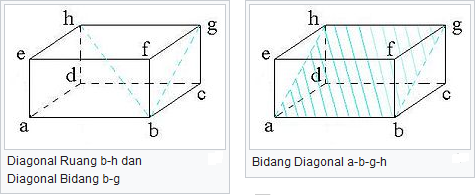
Pengertian / definisi Balok: Balok adalah bangun ruang tiga dimensi yang dibentuk oleh tiga pasang persegi atau persegi panjang, dengan paling tidak satu pasang di antaranya berukuran berbeda. Balok memiliki 6 sisi, 12 rusuk dan 8 titik sudut. Balok yang dibentuk oleh enam persegi sama dan sebangun disebut sebagai kubus.

Volume balok	: V = p x l x t
Luas permukaan balok	: L = 2 x ( pl + lt + pt)
Panjang diagonal bidang	: Db1 = √s2 +s2)
	: Db2 = √s2 +s2)
	: Db3 = √s2 +s2)
Luas bidang diagonal	: Lb1 = dB1 . t
	: Lb2 = dB2 . l
	: Lb3 = dB3 . p
Diagonal ruang	: dr = √( p2+ l2 + t2 )
Keliling balok	: K = 4 x (p + l + t)

Keterangan:

V	: volume
p	: panjang
l	: lebar
t	: tinggi
dr	: diagonal ruang
K	: keliling balok

3. Prisma Segitiga

Pengertian / definisi Prisma segitiga: Dalam geometri, prisma adalah bangun ruang tiga dimensi yang dibatasi oleh alas dan tutup identik berbentuk segi-n dan sisi-sisi tegak berbentuk persegi atau persegi panjang. Dengan kata lain prisma adalah bangun ruang yang mempunyai penampang melintang yang selalu sama dalam bentuk dan ukuran. Prisma segi-n memiliki n + 2 sisi, 3n rusuk dan 2n titik sudut.

Prisma dengan alas dan tutup berbentuk persegi disebut balok sedangkan prisma dengan alas dan tutup berbentuk lingkaran disebut tabung.

Volume prisma segitiga	: V = luas alas x t
Luas permukaan prisma segitiga	: L = keliling alas x t + 2 x luas alas segitiga

Keterangan:

V	: volume
t	: tinggi
L	: keliling
luas alas	: luas segitiga

4. Limas Segiempat

Pengertian / definisi Limas Segiempat: limas adalah bangun ruang tiga dimensi yang dibatasi oleh alas berbentuk segi-n dan sisi-sisi tegak berbentuk segitiga. Limas memiliki n + 1 sisi, 2n rusuk dan n + 1 titik sudut. Limas yang alasnya berbentuk segiempat disebut limas segiempat.

Volume limas	: V = 1/3 x p x l x t
Luas permukaan limas	: luas alas + luas selubung limas
Luas selubung limas	: luas alas + (1/4 × Keliling alas × t segitiga )

Keterangan:

V	: volume
p	: panjang
l	: lebar
t	: tinggi

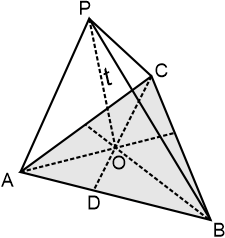
5. Limas Segitiga

Pengertian / definisi Limas Segitiga: limas adalah bangun ruang tiga dimensi yang dibatasi oleh alas berbentuk segi-n dan sisi-sisi tegak berbentuk segitiga. Limas memiliki n + 1 sisi, 2n rusuk dan n + 1 titik sudut. Limas yang alasnya berbentuk segitiga disebut limas segitiga . Limas segitiga adalah bangun ruang berjenis limas yang mempunyai sisi alas berbentuk segitiga.

Volume limas segitiga	: V = 1/3 x luas alas x t
Luas permukaan	: L = Luas alas + Luas selubung limas

Volume (V)	: V = ⅓ × La × t
	: V = ⅓ × (½ × as × ts) × t
Luas Permukaan (L)	: L = L alas + L ΔI + L ΔII + L ΔIII
Tinggi (t) :
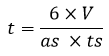Alas segitiga alas (as) :
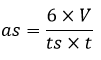Tinggi segitiga alas (ts)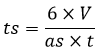
Luas Alas (La)	: La = ½ × as × ts
Luas ΔI	: L ΔI = ½ × a Δ1 × t Δ1
Luas ΔII	; L ΔII = ½ × a Δ2 × t Δ2
Luas ΔIII	: L ΔIII = ½ × a Δ3 × t Δ3

Keterangan:

t	: tinggi limas (PO)
as	: alas segitiga (AB)
ts	: tinggi segitiga alas (DC)
t1, t2, t3	: tinggi masing-masing bidang tegak
a1, a2, a3	:  alas masing-masing bidang tegak

6. Tabung

Pengertian / definisi Tabung atau silinder : Tabung atau silinder adalah bangun ruang tiga dimensi yang dibentuk oleh dua buah lingkaran identik yang sejajar dan sebuah persegi panjang yang mengelilingi kedua lingkaran tersebut. Tabung memiliki 3 sisi dan 2 rusuk.

Volume tabung	: Luas alas x tinggi
Luas alas	:
Luas selimut	:
Luas permukaan                 :	${\displaystyle =\pi d(r+t)}$ ${\displaystyle =2\cdot \pi r^{2}+2\pi r\cdot t\,}$, atau ${\displaystyle =2\cdot \pi r\cdot (r+t)}$
Luas permukaan tanpa tutup :	${\displaystyle =\pi r^{2}+2\pi r\cdot t}$ ${\displaystyle =\pi r(r+2\cdot t)}$
Rumus Volume Tabung	: V = π x r2 x t

7. Kerucut

Pengertian / definisi Kerucut : Dalam geometri, kerucut adalah sebuah limas istimewa yang beralas lingkaran. Kerucut memiliki 2 sisi dan 1 rusuk. Sisi tegak kerucut tidak berupa segitiga tapi berupa bidang miring yang disebut selimut kerucut.

Luas alas	:
Luas selimut	:
Luas permukaan	:     ${\displaystyle =\pi r^{2}+\pi rs}$, atau     ${\displaystyle =\pi r\cdot (r+s)}$
Volume	:

8. Bola

Pengertian / definisi Bola : Dalam geometri, bola adalah bangun ruang tiga dimensi yang dibentuk oleh tak hingga lingkaran berjari-jari sama panjang dan berpusat pada satu titik yang sama. Bola hanya memiliki 1 sisi.

Luas permukaan	:
Volume	:

Share :